PyRAT sails in to verify your neural networks

Performing formal verification of mission-critical software

Machine learning, especially through artificial neural networks, is currently undergoing an impressive expansion, penetrating fields ranging from driving assistance to legal or medical assistance. While seemingly beneficial, this revolution is causing concern as it approaches real-world application in mission-critical software, as the fragility of these learning techniques is increasingly exposed, particularly in the face of malicious disruption. Some work is already underway to adapt formal methods, used for decades in the field of critical software, to these new technologies.

This is what is envisioned with PyRAT, a neural network verification tool developed at CEA by the AISER team (which focuses on AI Safety Engineering and Research). Its development was motivated by the difficulty we found in linking some tools with our neural networks but also with the aim of facilitating the integration of verification process in the whole neural network development process. Our belief is that the main-streaming of safety practices in the development process can only be beneficial to neural network and AI systems as a whole and can increase our trust in them.

With its second participation to the International Verification of Neural Networks Competition (VNN-COMP 2024), PyRAT improved its ranking of last year, reaching the second place, by participating in all 12 benchmarks of the regular track and proving more than 1700 properties.

Catching the winds of abstract interpretation

Adapting state of the art approaches to tensor operations

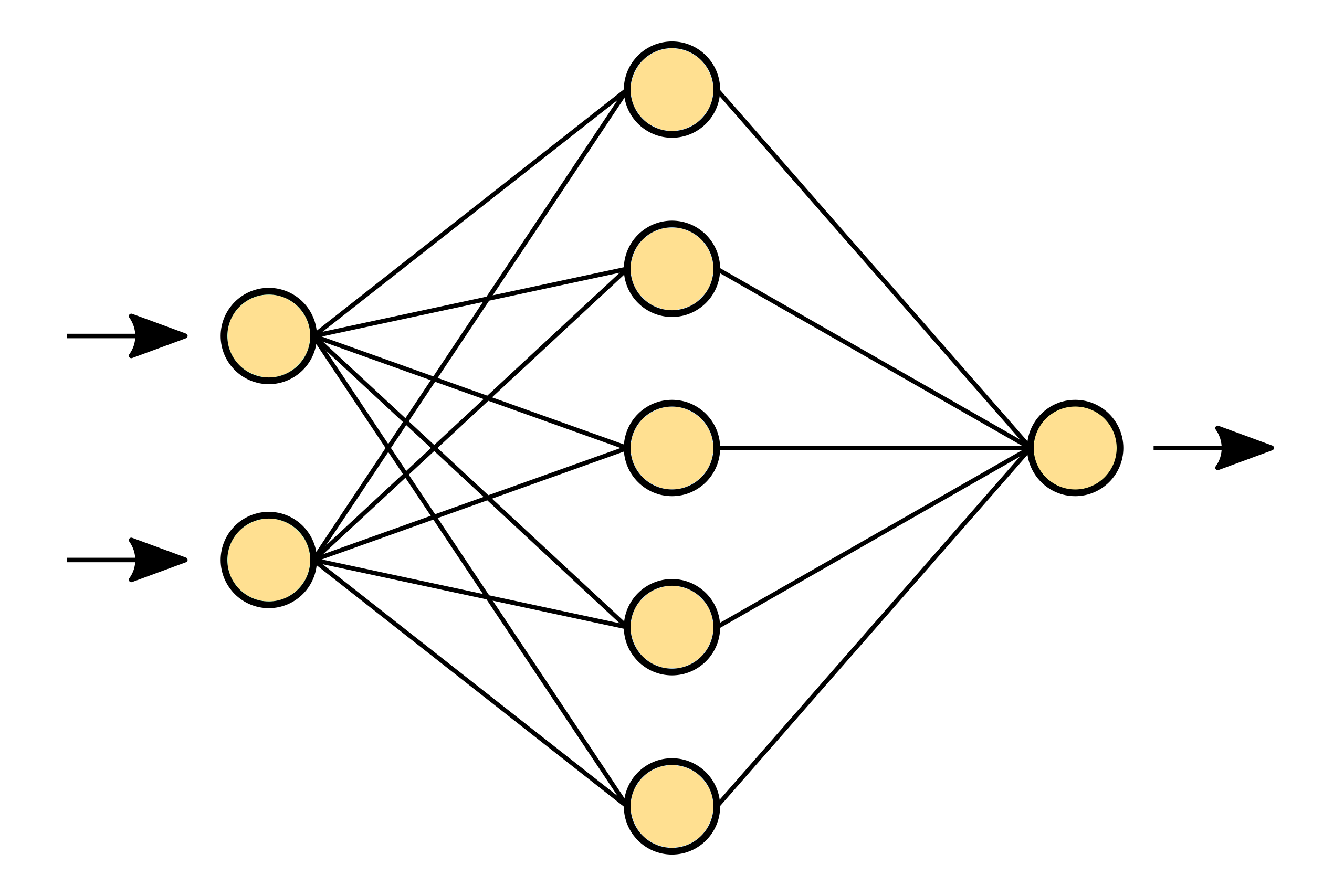
PyRAT stands for Python Reachability Assessment Tool and is based on abstract interpretation techniques with the aim of determining whether in a given neural network a certain state can be reach by the network from some initial parameters.

To do so, it propagates different types of abstract domains along the different layers of the neural network up until the output layer. This approach will overapproximate some of the operations of the layers and thus the output space reached will always be bigger than the exact output space. If the output space reached is inside a certain space defining the property we want, then we can say that the property is verified. Otherwise, we cannot conclude.

Through plunder or pillage

What do we verify?

Local robustness

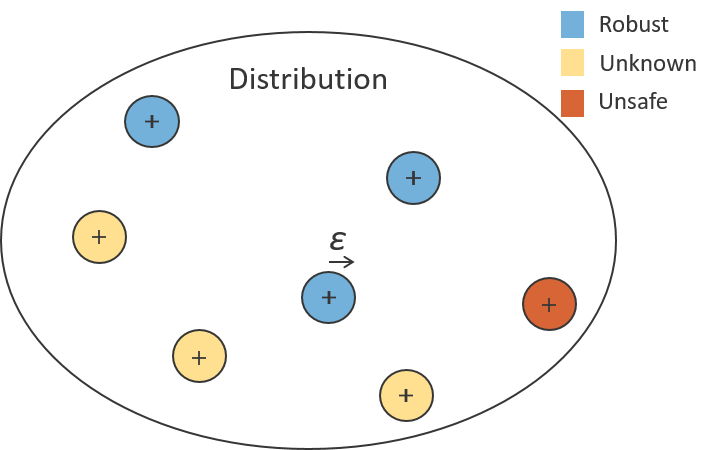
For all the points of a dataset, we verify their neighbourhood parametrized by a distance ε.

Here we can formally prove that for any perturbation inferior to ε the classification remains the same, i.e. the neural network is robust around this point. If a counter-example is found the neighbourhood is proven to also be unsafe.

Safety properties

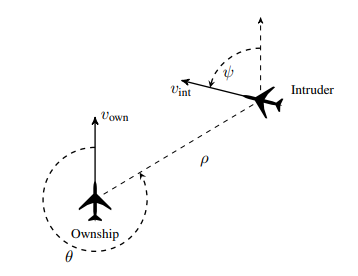
On the other hand we can prove more general safety properties, like here on the public ACAS-XU dataset and neural networks. In a setting of critical system of aircraft collision avoidance, we aim to prove that for certain configurations of the two planes the neural network will answer as expected.
For example, we could aim to prove:

∀θ∈[0,π2],vint,vown,ρ,ψ  ⟹  Neural network says turn left \forall \theta \in [0, \frac{\pi}{2}], v_{int}, v_{own}, \rho, \psi \implies \text{Neural network says turn left}

PyRAT from bow to stern

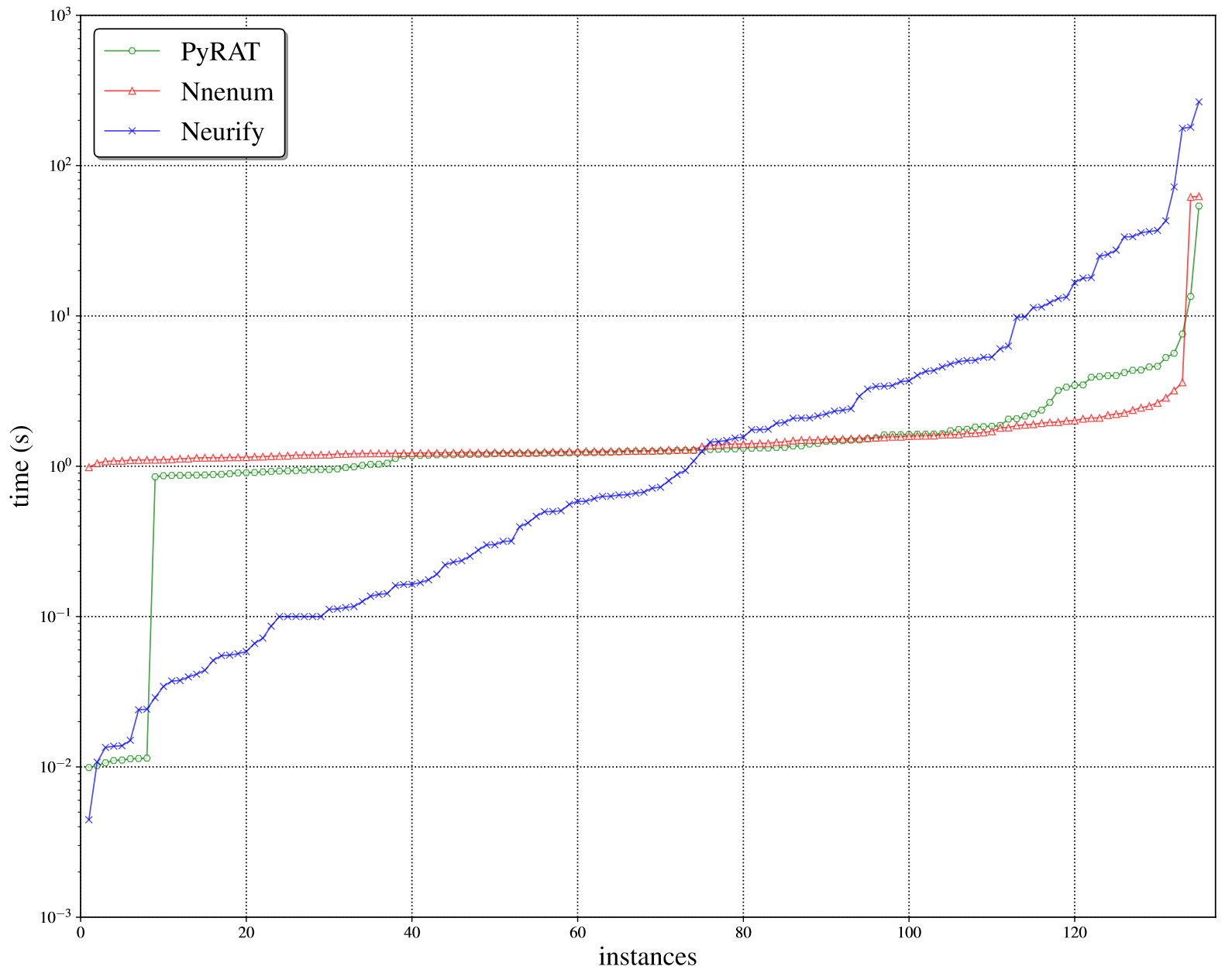
Wide support and state of the art performances

Due to an approach tailor made to neural networks and their high dimensionality, PyRAT is able to apply abstract interpretation techniques while fully leveraging tensor operations.
A wide range of neural networks and their layers are already support in such forms in PyRAT with possibilities ranging from simple and small tabular problems and networks, to complex architectures with convolutional layers and skip connections. Thanks to this, PyRAT is able to show comparable result to state of the art verification tools and even outperforming some on certain benchmarks.

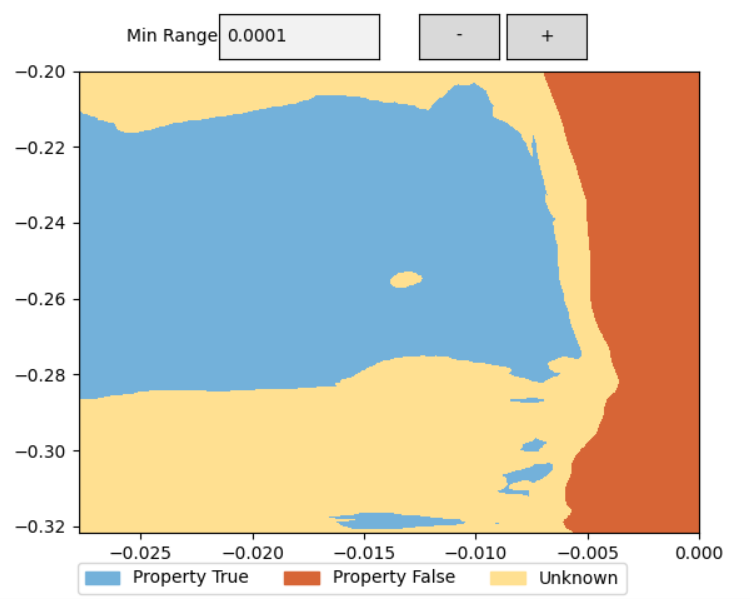
Specifying the property and visualising the result

Through its own expressive property language or the VNNLib format, PyRAT allows to specify safety properties to verify over a neural network.
Following its specification, one can visualise with PyRAT the result of an analysis with modulable precision on this property. This visualisation will show the safe, unknown and unsafe spaces corresponding to this property. In turn, this will allow to either refine the property or identify the gaps in the neural network training.

Input partitioning

Another key aspect of PyRAT lies in the input partitioning mechanisms that it employs. For lower dimensionality inputs, PyRAT is able to use input partitioning as a mean to increase the precision of the analysis and prove a wider range of property. This partitioning is reinforced by heuristics tailored to the abstract domains we use which allows a significant boost in precision on such networks